From the Author: Michael Banjanin
(i) Introduction
(ii) Basic Structure
(iii) a. Geometry of the Framework
(iii) b. Fundamental Laws
(iv) Order of Electron Energy Levels
(v) a. Secondary Relations
(v) b. Interdisciplinary Relations
“in the beginning…”
(i) Introduction
What began back in February 1991 (an exercise which sought for a relationship between Biblical numerology and physical science) as a “stab in the dark,” turned out to provide the basis for a lifetime of work. While trying to establish comparisons with atomic periodicity (inturn re introducing myself to the Periodic Table) I became disgruntled with the old design. Having an interest in unified theories gave me the idea to search for a Unified Table of All Matter or Universal Building Block, then after a year of part time research the first stage or two dimensional form of the Progressive Periodic Table of the Elements (PPTE) was created. As time progressed so did the table; what started as an exercise, soon became a study into the old discipline of Periodicity destined to once again see light of day. Since it’s conception the PPTE has been regarded by many, as one of today’s most exciting and successful developments aimed at improving the current form of the Periodic Table. It has received positive reviews by academics in the fields of Inorganic Chemistry and Theoretical Physics and is continuing to attract interest throughout the world.
If improvements to the original table are to be accepted, it’s important that these changes be in accordance with the physical laws that govern Atomic structure. Since the discovery of the Periodic Table many advancements had been made throughout science as a whole, so much that a complete overhaul of the table deserves to be implemented. With this in mind whatever the outcome, it would be expected that any new developments would also (in time) be superseded, which is after all the nature of discovery. It is my belief that as interest in this Universal Periodic Table grows, so too it’s development as an Inter Disciplinary Link, similar to Einstein’s Relativity but containing much more physical information with a larger participant interest. For the PPTE is Unified Theory according to Geometry. This automatically appeals to a wider audience (ie. more visual, less numerics) and by including all facets of science, invites the scientist or student to participate in adding to a Unified Theory within their field, without the need of being a genius in Theoretical Physics. Now I’m not trying to play down or trivialise this field of study which among the disciplines holds my greatest respect, but merely trying to tackle this problem from a different perspective as well as utilising the expertise of the individual, whose field may not be as wide as Theoretical Physics, yet whose knowledge of the finer details may contribute to improving our understanding of the relationship of matter, according to it’s relative position (geometrical) in this proposed continual periodic table of all matter (continuum).
Following as best described by me, is a simplified explanation of the differences between this new table and the old, as well as the reasoning for the changes; in a language the student, scientist or layman may understand.
“I would rather speak five intelligible words to instruct others than ten thousand words in a tongue.”
(ii) Basic Structure
Throughout my research of different table designs certain key features were much desired by their creators. Most importantly was of course the grouping of the Elements (atoms according to their number of protons) with their same type of electron shells (Periods K,L,M…) and sub shells (Groups s,p,d…) which were preferred to be positioned one after the other according to their proton number. What was also desired was for this line to be unbroken travelling in a spiral direction much like a staircase. In previous designs we find periodic spacing in the framework of these tables or gaps between certain elements; sometimes lines were also placed in order to show alignment between elements, which defeated the reasoning for those particular styles of tables to be adopted. In fact to my knowledge apart from the PPTE there is no other complete Isotopic table that aligns the elements in a continual line or string while still keeping the original links between the electron shells and sub shells.
“Beauty is in the eye of the beholder”
To better grasp the difference between the current table and the PPTE, imagine if a group of students were being taught the anatomy of a human where half of the head was drawn on the left hand side of the page and the other half on the right, with half of the body being separated along with it, then imagine the whole body being squashed to one third its original height; but it doesn’t end there, the feet were connected to the pelvis and the legs were drawn separately on the side of the page because at the scale in which it was drawn, the whole body couldn’t fit on an A4 sized page! The unfortunate side to this story was that when the real McCoy came along they failed to recognise him. The ridiculous side to the story was the fact that some still preferred the original disfigured thing on the basis that McCoy had a blemish on his face thus rendering him imperfect! As strange as this may seem it is the closest analogy to the comparison between the PPTE and the current table in use. I personally have a deep feeling of respect for the contributions our scientific forefathers have made but also honestly feel the need for improvement as they had improved on the theories of their day.
(iii) Geometry of the Framework
Let us assume that if we were to take a piece of space and plot a family of particles within it’s boundaries, certain constraints would need to be implemented (or features of the particles need to be grouped), if we are to expect it to show any regularity or periodic similarities between the particles. Secondly since mathematics is the language in which the geometry of space and life is expressed simple mathematical rules shall also be applied to test our model or act as an added constraint.
To begin let us start with a number line, in this case our particle is the Atom which consists of three of the most stable particles for their size, known as the Proton, Neutron and Electron. What we find is that when we alter the number of protons the atom changes in it’s outward appearance more dramatically than when we change the number of neutrons, but what we do find is that when the ratio of neutrons on average decreases from one proton to one neutron or increases from one proton to two neutrons the atom becomes highly unstable and begins to break down (radioactivity). So even though the neutron has important characteristics in it’s make up for now we shall look at the most obvious features of the atom due to the proton.
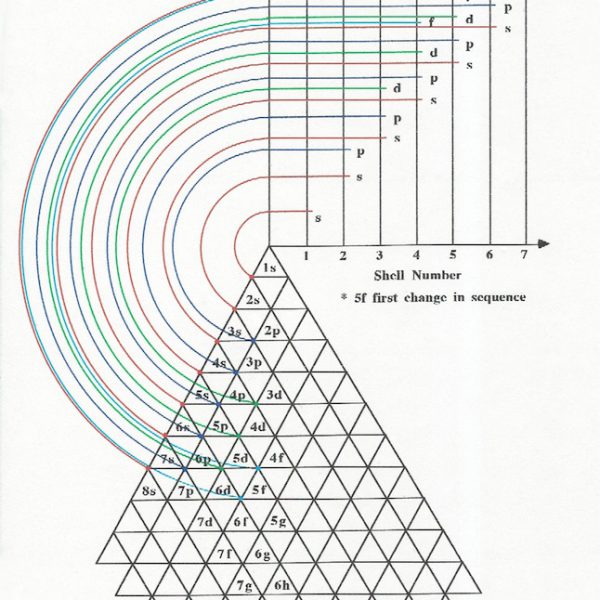
As the proton in this case is our measured unit we shall divide our number line into equal parts directly corresponding one part to one proton. As it was discovered after placing the Elements (Atoms according to their number of protons) in a grid pattern in rows of eight, certain similarities between elements in the rows and those in the columns became apparent with the way each element chemically reacted. The problem at this stage was the constraint of keeping to the number line, but for now lets continue; as research discovered the original group of eight needed to be extended to eighteen which incurred a further separation of the number line so that. The horizontal lines would still link elements of similar shell type (Periods) as well as linking elements in their vertical columns of similar sub shell type (Groups). Later as the table filled even further the columns or Groups needed to be extended to thirty two thus showing a consistent growth rate between the shells. If we’re to view this rate we find that between paired periods the protons increase at 2n2 or 2,8,18,32,50… . So what we find unless we gradually decrease the size of the units we’ve designated in the grid, the rectangular shape will have to change.
“Still other seed fell on good soil, where it produced a crop 30, 60 or even a 100 times what was sown.”
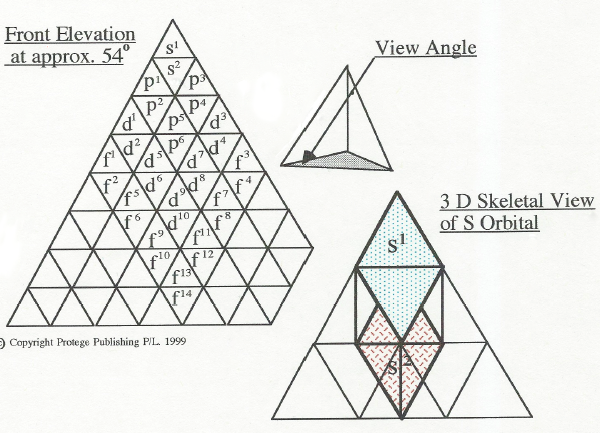
By deciding to keep the grid units uniform, our next step is to change the overall shape to a triangular form so as to accommodate the increasing numbers of elements per shell. But as far as the grid units themselves are concerned lets not haphazardly jump to the first shape that comes to mind without confirmation from the abundant wealth of information that we have accumulated over the past 100 years. Since we’re dealing with shapes in two dimensional form lets start with the circle, being a fundamental shape, by stacking these on top of each other in this triangular fashion. What we find is that as with snooker balls it increases at the rate of n[(n+ 1) / 2] or 1+2+3+4+5… or 1,3,6,10,15… But what of the space between the circles one might ask, well in actual fact we find this pattern in things like sunflowers, bubbles and honey cones, the difference is that when circles of equal size are evenly squashed together they make an hexagonal shape; which also just happens to divide up into six equilateral triangles. We can also find these shapes in molecules and their crystal formations, even squares can be divided into triangles. Some at this point may choose to argue a case for the humble triangle as to be used as our periodic guinea pig, but before we take this route there is one other piece of evidence for the use of the triangle; funny enough it comes in the form of a periodic table.
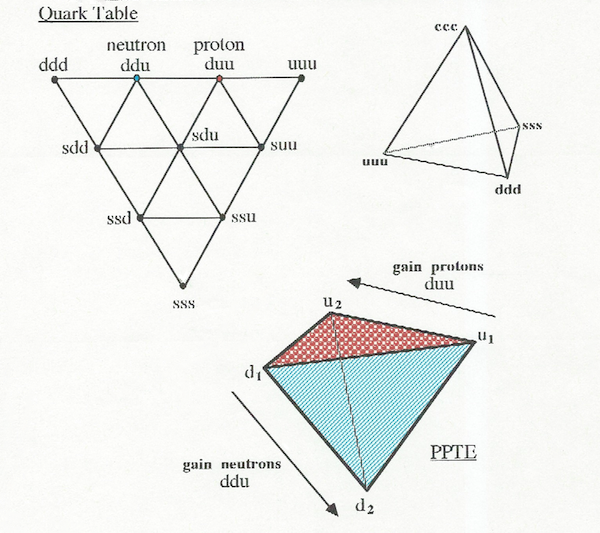
Quantum electro dynamics I must admit sounds and generally is presented bland and scientifically sterile or incomprehensible, this is because it’s still a relatively new subject, but the structure of these smaller particles are very similar to the atoms, for they’re directly related as a body is with it’s organs and what I’d found helped piece this puzzle together. By looking into the material that make up the protons and neutrons we find interesting particles known as quarks; well back in the sixties Murray Gell-Mann & Yuval Ne’eman developed a periodic table for quarks which was named “The Eight Fold Way. ” Now quarks in their most stable form exist in pairs (Mesons) and triplets (Baryons) and in a variety of forms and combinations, in this exercise we shall talk about only four different forms they are up(u), down(d), strange(s) and charm(c), and of these four for now we shall point out two in particular the u and the d quarks. What was found is that the proton is made up of the triple quark combination duu and the neutron is made up of the triplet ddu; the most interesting thing about these particles is that the periodic table designed for them is in the form of an equilateral triangular grid!
From this point I was convinced that by introducing an equilateral triangular grid to the multiple string form I was working on, a viable solution could surface, as it did; but it didn’t end there for as I had found later the quark table of triplets consisting of protons and neutrons was actually a three dimensional Tetra Table or Tetrahedron governed by the four forms u, d, s and c at the vertices or points of the table. This gave me the initiative to extend the PPTE to 3D. which allowed me to include the neutrons, hence a complete Isotopic (Elements with different numbers of neutrons) table.
Now for a first, the continuation of a periodic table ranging from quarks to atoms to molecules! Like domino’s the pieces fell together but at this stage it’s easy to get ahead of ones self without refining the conjecture. As much as I could taste the victory of getting so close to a Unified Table of All Matter, my initial desire; now had to wait until the loose ends were tied up.
“Patience is a virtue!”
(iii) b. Fundamental Laws
No matter how lovely an idea is (or table in this case), without the language of numerical law there to back you to the hilt, the idea loses it’s scientific relevance. So far I’ve mentioned the need for a spiralling (unbroken) string of elements and the preferred shape of the table, yet to truly understand the numerical reasons behind this, we need to understand the way numbers relate with geometry (form, shape) and the formation of matter (everything).
Socrates an ancient observer of life (scientist of his time) stated that “God wrote the universe in the language of numbers,” indeed everything we have studied has shown a make up of numerical progressions of smaller particles; in most cases we find these progressions spiralling in an unbroken line, throughout the entire body of the object of study ie. crystals, D.N.A ., plants…etc. To understand why, imagine a group of people building a lighthouse, they start building at the rate of one brick at a time, this is simply represented as our number line or continual string (1,2,3,4…), as they get higher they reduce the number of bricks per level so as to give the structure added strength reducing it’s chances of collapsing this is represented as our progression (starting from the bottom 100,99.5,99,….70 bricks top level); when they get to a height where they cannot reach they decide to build a ladder, but they find the climb difficult, then one suggests building a spiral staircase in which they find the climb easier and much more productive.
When we look at matter in general we notice it too finds the line of least resistance not only for it’s creation but for other reasons such as, the reinforcing against external resistance, in this form the strings of material form a mesh type appearance, running diagonally along the member winding clockwise and counter clockwise. In biological studies the form of engineering known as tensegrity also shows how life itself utilises geometrical form which to this day continues to inspire researchers to develop better design for human applications. Hence the importance for the existence of the spiral, which persistently reappears throughout all matter.
Now that we’re clear on the significance of the (1) unbroken string (number line) (2) progression and (3) spiral action; we can now dedicate this next part directly to the division or distribution of energy and matter in measured space, according to the most fundamental aspects of geometry and the laws of physics. For those who may feel alienated from understanding the last phrase I promise by the end of this chapter you will fully comprehend the meaning and significance this has with the periodic table.
“I fought the law and the… law won.”
At the beginning of chapter (iii) I spoke about taking a piece of space and plotting the elements according to their characteristics which I called constraints. What we’re talking about is placing the atoms on a table where atoms with similar body parts are grouped together, the most predominant or visible parts of the atoms are the electron shells, in which the electrons occupy the space around the nucleus (protons and neutrons). These shells can be compared to onion rings or floors (as in an apartment building) which we call periods with the designated symbols K,L,M,N,O,P,Q… The mathematical letter used to represent these shells in our equations is the lower case letter (n) known as the first or Principle Quantum Number , ie. when (n)=l we are referring to the 1st period or K shell, when (n)=2 we’re talking about the 2nd period or L shell and so on. The letter (n) in maths usually stands for any individual number from the most common of all progressions 1,2,3,4,5…, this is the reason (n) is used with the shells.
When we count the max. amount of electrons that can fill these shells we see that it follows the formula 2(n) ² or 2,8,18,32,50,72,98… If we check this with the M shell we find n=3 therefore 2(3 x 3)=18 which is correct, for in the third shell the max. electrons it can hold is 18. This becomes our first constraint, in other words on our table when we group the elements (atoms according to their proton number) these shells shall be grouped as a first priority for they are one of the most obvious parts to the structure that contain the electrons, that’s why it’s called the PrincipleQuantum Number. I shall also refer to them as the floors of a building
“Foxes have holes and birds of the air have nests…”
The next most important feature to the atoms are the subshells, which are like apartments on the floor of a building. Now each shell is made up of one or more subshells which are also known as groups and these are designated by the lower case letters s,p,d,f,g,h,i.., where the number of subshells per shell is also governed by the value of (n) ie. If we look at the M shell, n=3 therefore the M shell has three subshells s,p and d. This brings us to our next constraint or body part. Therefore by imagining the atom like a spherical (ball shaped) building and the shells like floors then it’s understandable why the subshells or apartments could then be considered as the next most important item, which are identified by the second or Orbital Quantum Number. What we find is that with electrons (like living organisms) though they may have a whole floor in which to roam, once placed amongst fellow electrons prefer a room of their own and stay in their rooms until their roused or get excited. Then if the subshells are referred to as apartments then each apartment is divided into rooms, and in the subshell these rooms are called Orbitals. The mathematical letter used to represent these orbitals in our equations is the lower case letter ( l) which also stands for the Angular Momentum or 3 dimensional shape of the orbital. Each subshell has a set number of orbitals or rooms and even though they may not be occupied by electrons they’re presence is still recognised and at times utilised by excited electrons.
Each one of these orbitals may contain 0 , 1 or 2 electrons at most. In the case of 2 electrons they must be opposites which we’ll discuss later. As with the shells the subshells also follow a formula, where in this case the l values for s=0, p=1, d=2, f=3… and the max. number of electrons per subshell is 2(2l +1) or 2,6,10,14,18,22,26… Therefore the formula for the orbitals per subshell would be half the electron amount 2l +1 or l,3,5,7,9,11.. and the same for orbitals per shell, 2n ² becomes n² or 1,4,9,16,25,36,49… The relationships are much clearer when viewed together eg.
As a result of this section we can now see the order in which the electron shells form around the nucleus and the simplicity behind their numerical sequences. What scientists have discovered is throughout all of matter certain numerical progressions are found in its fundamental make up. With this in mind unified theories linking all matter became much sought after because it became apparent to scientists the further we look away the more related everything seems to be. Out of these theories came some of the most fundamental laws which reach out beyond that which we have discovered. One of these laws I would like to explain in more detail, because what I had found seemed to bridge the gap or show a relationship between the elements and the tetrahedral pattern I’ve chosen to house the elements in.
Imagine if you were standing next to a light source, say 1 metre away and you had an apparatus in your hand with which you could measure the luminosity of the light; lets say it was 1 lux (unit of illumination). Then if you were to move to 2 metres away the luminosity of the light would decrease to 1/4 lux, and at 3 metres the luminosity would be 1/9 lux. What we find is that light separates according to the square of the distance. his division or distribution of energy is known as the Inverse Square Law. In fact this law is found to be effective amongst forces such as gravity and magnetism as well.
To better understand this we shall turn to geometry for some answers. Let’s for this instance take a sphere or say a ball bearing with a radius of 1cm, when we calculate the surface area (4pi r²) it amounts to approximately 12.56cm²(or 1 square unit), next if we calculate the surface area of a ball bearing with a 2cm radius it amounts to 50.26 cm²(or 4 x 1 square unit) and again the surface area at 3cm radius is about 113.09 cm²(or 9 x 1 square unit). Again we see that the differences between the areas are multiplied by the squares of the distances. In the case of our light bulb if the area at 3 metres away is 9 times greater than at 1 metre then it’s understandable why the light particles would be 9 times less numerous or 1/9 the luminosity than at 1 metre away. This is an undisputable relationship between geometry and the way matter sorts it self out. Thus as we see a pattern of squares appear in the make up of the atoms we can then determine with a high probability that the atoms are ordered or created according to this fundamental geometric pattern.
As can be seen previously in diagram 2 when we look at the area of the triangular grid pattern, the individual triangles per level always add up to the square of the distance. This I believe is a suitable starting point for housing the elements, for this most basic geometric shape also allows for experimentation as well as change. What I had also found interesting about this geometric relationship is that by carefully analysing the 3 dimensional make up of the tetrahedron more characteristics of the atoms could be determined by linking them directly with the patterns in the tetrahedron. An example of this is observed by counting the volume of units in a tetrahedron. At each level the progression grows according to the cube of the distance (n³) or 1,8,27,64… when we observe the Stabilising Force of Atomic Nuclei we find that the energy distribution of this force is also dispersed according to the cube of the distance, this proportional division we may then call The Inverse Cube Law, which further cements our geometrical relationship with the Atoms as well as show the Tetra Tables unique ability to bring to the forefront general relationships through simple observation
From this point we move to the next part of the Atom which deals with the orientation of the Orbitals known as the third or Magnetic Quantum Number. It’s identified by the lower case letters (mi) or just (m) for short. This is simply the angle at which the orbitals are in relation to the nucleus (protons/neutrons). These values are also covered by the formula 2l +1 or 1,3,5,7,9,11,13…, therefore in the f subshell, the l value is three and by applying the formula we calculate 2×3+ 1=7 which is correct for there are seven orbitals in the f subshell and also seven different possible orientations which depend on the number of electrons that are filling the subshell. When we look at diagram 2 we see that the area per level grows according to this same sequence, and the squares are the total areas per level eg. 1+3=4, 1+3+5=9, 1+3+5+7=16. So now this table also shows the relationship between the orbital numbers and the Inverse Square Law.
Now to the final part of this chapter which deals directly with the electrons known as the fourth or Spin Quantum Number. This is identified by the lower case letters (ms) or just (s). The very thing which separates electrons from each other is their similar pole or charge but like the majority of living creatures they prefer to join with their counterpart or so to say their opposite type sex, the difference between them is the direction in which they spin or rotate about their axis. Their values are either +1/2 (spin up) or -1/2 (spin down). When we look at the triangle configuration of Diagram 2 we see a clear distinction between the shaded triangles (pointing up) and the unshaded triangles (pointing down) which not only relates to the odd/even numbers of the protons/electrons but in this case also signifying geometric opposing parity within the Atom.
Previously I talked about the way energy disperses according to the inverse square or cube of the distance, with the electrons however there is another force known as the Magnetic Dipole Force which dissipates to the Inverse 4th Power of the distance (n4). Again the triangular configuration shows this same ratio when reading point 4(b) in Diagram 2. In this case the area prior to each period pair grows at this same rate n4 or 1,16,81,256… signifying distinctive changes to the shell structure according to this ratio.
Therefore to summarise this chapter conservatively, we may safely state without ridicule, that we have been able to see distinctive relationships between the PPf E and the four Quantum Numbers; as well as linking three specific forces that govern the Atom, to the geometric shape and pattern of the PPfE; this is why I believe the PPf E is today’s most accurate account of the periodic organisation or division of Atomic matter in measured space.
“A cord of three strands is not quickly broken”
(iv) Order of Electron Energy Levels
Here we have another clear example of a three axis table linking elements in 2 dimensions but still not without certain discrepancies. As the order suggests s, ps, dps, fdps… when we reach the 5f subshell we find it sneaks in between 6p and 7s. Again I applied the triangular table to the order of electrons and as your about to see the geometrical positioning clearly shows this change in order.
In this form the positioning of the electrons takes on a more acceptable format showing both the periodicity of the shells as well as the energy levels in their proportional order, but most importantly revealing the hidden understanding of why certain shells fill outside of the conventional f, d, p, s order.
To follow suit with the PPTE, I applied this format to a 3 dimensional model thus including all the electrons, most importantly was the need to account for the total cubic volume in electron units ie. Allocating a measured unit of space for each electron that may fit neatly within the constraints of the tetrahedron. As I had mentioned before with packing circles together the bonding force or pressure changes the shape of the circles into hexagons with its area staying the same. With orbitals their shape changes dramatically as the electrons fill each orbital, where as their energy levels do not vary much at all within the same subshell; as with the circle it’s not always the shape that’s important but the amount of space it needs to occupy. Until you actually hold a multiple layered tetrahedral frame in your hands trying to imagine the coordinates even with diagrams tends to get a bit confusing.
In this model I chose the hexahedron or stretched cube as our orbital guinea pig because when multiplied its geometry fills the entire space within the tetrahedron, also as this type of cuboid consists of two opposing tetrahedrons along with an octahedron (truncated tetrahedron, diamond or double pyramid base to base) in the centre, it seemed to fit the up and down characteristics of the electron comfortably.
“You can choose your friends …”
(v) a. Secondary relations
One of the things about the PPTE I haven’t spoken much about are the secondary relations the elements have regarding their chemical properties. It is interesting to note that the J J Thomson I Neils Bohr preferred alignment of the elements are placed in similar order as the PPTE where the difference, lies in the spacing of the grid. Between the elements lines were drawn linking the subshells on the top side and another series of lines linked the elements with these secondary relations on the bottom and elements of the same shell were linked vertically. This clearly demonstrates a valid reason for including a third axis to the periodic table and as seen in the previous tabled Order of Electron Energy Levels, again the horizontal axis shows the basic order in which the subshells fill (our number line), the left axis link elements with the same shell (our first constraint or body part) and the right axis link elements with the same subshell (our second constraint), this is periodicity at it’s simplest and to some degree it’s best. But we can’t leave a job half finished, for now that the most obvious features of the atom have been covered and since the humble triangle won the war of law on the proton plane, it would be a reasonable suggestion to extend this two dimensional table to 3D to allow for the neutrons. You see once we refuse to leave anything out, everything begins to fall into place, and as an old saying states, “You can choose your friends but you can’t choose your family,” in this case by accounting for all the particles, proved to benefit our results.
Since the protons and neutrons are very similar in composition I believed for the time being we should use the same sized unit as we do for the protons. This was a fairly straight forward exercise which introduced columns of equal sized units running vertically (approx. 54 degrees) from each element like adding a z axis to an existing x,y plane. This meant that the neutrons did not change the proton order in any way but merely gave it depth or altitude. It also meant that geometrically the neutrons could behave quite differently since they were operating on an opposing plane.
(v) b. Interdisciplinary Relations
At this point we need to go back to chapter (iii)a. for a moment, for as I’d explained before, protons and neutrons are triple Quark combinations or better known as Baryons. Since we already have a tried and proven periodic table for quarks it stands to reason that part of it’s form may be able to assist us in developing our table, with the hope of integrating the two together.
We could also work either way; of having the quark table larger or smaller than our atomic table. In this case I’ve opted for the larger reasoning that there’s a greater abundance of smaller particles and that it’s their laws which govern the development of the larger particles. In the diagram below you can see the floor plan to the quark table and to the right of it the tetrahedral version (simplified) with the four major quark co ordinates up, down, strange and charm (u,d,s,c). Below this you will also see the PPTE and notice that I’ve given it four co ordinates, as it suggests the plane running along the d1, d2 edge belongs to the neutron plane, for each neutron consists of two d quarks and one u quark and the opposite plane running along the u1, u2 edge belongs to the proton plane, for each proton consists of one d quark and two u quarks. I figured as with the quark table the co ordinates of the plane could then signify the particle, therefore it not only shows the direction of multiplied particles (spiral action) but also implies positions for every kind of exotic particle or combination that could exist (Isotopes).
As you can see the Quark table has no strange or charm quark presence in the proton/neutron region so therefore the four co ordinates on the PPTE are strictly governed by the up and down regions which would place the PPTE in a centralised position between the points ddu and duu in the Quark table.
It should be noted that this version of the Quark table is a superimposed copy of two tables (octet & decimet) where the proton and neutron belong to the octet a truncated tetrahedral table. The difference between the proton/neutron and their similar delta particles is their spin where as their quark combinations are the same. This was done purely for the sake of simplifying the overall co ordinates so that the reader may grasp the position in which the PPTE may sit as well as view the continuity the tetrahedron takes through the quark dimension.
When viewing the PPTE Tetra Table it should be understood that the entire space within the tetrahedron is co ordinated accommodating all the isotopes each in line with their element. In other words as a star with the potential of becoming a neutron star begins to compress, the possibility of isotopes exceeding their normal ratio of protons to neutrons (if but for an undetectable moment) still exists; therefore their positions need to be left open because of their possible existence; much like the artificial trans uranium elements which scientists continue to discover under extreme conditions eg. Even though a Hydrogen Isotope with 42 neutrons may never exist within this environment, a position for it none the less is allocated, for in the world of infinity “benefit of the doubt” goes a long way.
From here we can now multiply the PPTE in this case five times to complete a full rotation where the edge d1, d2 becomes the central axis and the edge u1, u2 becomes the outer circumference line where the PPTE resembles something like a segment of an orange. In this form five individual strings each a complete periodic table wrap around each other like a cord of five strands. By altering the shape of the units, designs with more or less strings can be created again without losing it’s periodic value. Thus from a two dimensional square rigid table with two axis we may now consider a three dimensional flexible string with four axis (1/ Shells 2/ Subshells 3/ Secondary relations and 4/ Isotopes) and a real opportunity for unifying the Atoms with their neighbouring particles Molecules and Quarks along the lines of an advanced geometrical periodic frame.
What we find is that the limits to how far we go with this concept of linking multiple disciplines via periodicity are strictly governed by our own imagination and as human technology continues to advance it is highly likely that we shall continue to identify periodic links throughout all forms of matter. At this stage I must draw this explanation to a close and return to developing the PPTE 3D version for CD ROM, the 3D straw model version and the PPTE wall chart. The work is extensive, time consuming and very expensive but we hope to have this available to you soon. If you would like to contribute to it’s development then by all means the best way you or your school can help is by purchasing the current table via an Academic Bookstore or School Supplier in your region and by debating it’s relevance with your class. Instead you may also choose to down load our mail order form and receive your copy via post, unfortunately this method is more expensive but at this stage may be your quickest option for obtaining a copy until we can manage to stock your region. Please do not hesitate to let us know how you feel about this product for every bit of encouragement goes a long way, yet every bit of criticism helps us even more.
I would like to thank you very much for taking the time, in considering this conjecture of mine and may this little information feed the fire of thought for the scientist who ought!
By Mr Michael Banjanin
Author of The Progressive Periodic Table of the Elements also speaking on behalf of Protege Publishing Pty .Ltd.
email:michael@goodperiodictable.com
The Progressive Periodic Table of the Elements.
Foundation for the worlds first Unified Table of All Matter…
GEO MET RIC
ORG ANI SED
DIM ENS ION . . . . . making sense out of chaos!